En France, l’apprentissage des tables de multiplication commence vers 7 ans. Les tables de 2, 3, 4 et 5 sont au programme du CE1, les tables de 6, 7, 8, 9 et 10 sont enseignées au CE2, avant d’être revues dans les classes supérieures.
Avec des méthodes scolaires basées uniquement sur la répétition mécanique, certains enfants éprouvent de réelles difficultés à mémoriser leurs tables de multiplication.
Je propose ici, dans ce dossier, des alternatives à cet apprentissage des tables égrainées une par une telle une comptine à apprendre « par cœur ».
Comprendre, manipuler, jouer : oui, il est possible d’apprendre ses tables de multiplication sans stress et avec plaisir !
Du côté des adultes, une certaine crispation autour des tables est observée. Certains parlent d’hermétisme aux tables de multiplication. D’autres disent n’avoir jamais réussi à retenir leurs tables étant « nuls en maths ». Ce discours d’adultes et de parents est parfois repris par les enfants. Mais souvent, il n’a pas lieu d’être. Sauf, peut-être dans des cas de dyscalculie ou d’autres troubles des apprentissages, tout enfant est capable de se référer aux tables de multiplication et de donner un résultat correct s’il est interrogé.
Pour se détacher de l’idée de l’apprentissage par cœur, vous trouverez dans ce dossier, des idées ludiques qui ont vocation à aider votre enfant à mémoriser ses tables mais surtout à lui (re)donner confiance en lui et en ses capacités d’apprentissage. Car le jeu est synonyme de plaisir et d’émotions positives, deux piliers essentiels des apprentissages.
« Le plaisir est non seulement un ingrédient de l’apprentissage mais son moteur, l’élément sans lequel il est impossible d’apprendre », écrivait, en 1997, Michel Lobrot, professeur émérite à l’université Paris VIII, auteur, chercheur et praticien en psychologie de développement personnel.
Si votre enfant a malgré tout du mal à retenir par cœur ses tables après avoir mis en œuvre toutes les idées que je vous souffle ici, il pourra contourner cette difficulté en retrouvant les résultats par des astuces que je liste en toute fin de dossier.
=> Le fil rouge de ce dossier : faire de l’apprentissage des tables de multiplication un moment agréable et ludique.
Sommaire
- Pour retenir ses tables, deux préalables sont nécessaires : comprendre à quoi cela sert et ce que cela représente
- Apprendre ses tables de multiplication en fabriquant ses propres outils et ressources
- Apprendre ses tables grâce aux pédagogies alternatives
- Réviser ses tables en jouant
- Réviser ses tables à haute voix
- Mettre les tables de multiplication en images
- Si l’enfant n’arrive toujours pas à retenir ses tables : des astuces pour retrouver les résultats
- Conclusion
Ce dossier est également disponible sous forme d’ebook téléchargeable :
https://6foisplus.com/telechargement-ebook-tables-de-multiplication
1/ Pour retenir ses tables, deux préalables sont nécessaires : comprendre à quoi cela sert et ce que cela représente
Apprentissage par cœur et compréhension des notions étudiées ne sont pas à opposer. Ces deux moyens d’apprendre sont plutôt complémentaires.
« Les deux sont indissociables ! Les recherches montrent qu’il faut valoriser l’apprentissage par cœur, mais que l’acquisition des connaissances fait nécessairement appel à la compréhension et à une mémoire du sens nommée mémoire sémantique. L’Éducation nationale doit s’emparer de ces enseignements », expliquait le chercheur Alain Lieury dans un article republié en janvier 2019, dans un numéro hors série du magazine Pour la Science dédié à la mémoire.
1.1 Comprendre à quoi sert de mémoriser ses tables de multiplication

Evidemment, ne pas connaître par cœur ses tables de multiplication ne représente pas un réel frein dans sa vie quotidienne. Toutefois, cela peut représenter un réel atout !
Imaginons la situation suivante : vous invitez vos voisins et leurs deux enfants à déjeuner, un dimanche midi. Vous serez, en tout, 9 à table. Vous devez composer le repas et prévoyez de servir deux filets de sole à chacun. Vous achèterez donc 9 fois 2 = 18 filets de soles (ou plus si vous souhaitez qu’il y ait du rab !). Cela ne vous aura pris que quelques secondes au supermarché pour réaliser ce raisonnement et trouver ce résultat. Car 2×9 ou 9×2=18 est resté gravé dans votre mémoire depuis votre enfance.
Et si ne pas connaître ce résultat par cœur n’est pas grave en soi, puisque l’on peut aisément compter 2+2+2+2+2+2+2+2+2=18, savoir que 9 fois 2 = 18 vous aura fait gagner du temps !
C’est un peu comme se rendre d’un point A à un point B à pieds alors que d’autres moyens de transport peuvent vous faire gagner un temps précieux.
Certains diront que cela n’est plus vraiment important aujourd’hui dans la mesure où nous nous baladons en permanence avec une calculatrice dans notre poche : notre smartphone. A cela nous apporterons trois réponses :
– Réponse n°1 : cela n’est pas toujours vrai, en particulier chez les enfants !
– Réponse n°2 : sortir son téléphone ou sa calculatrice ne fait pas toujours gagner du temps. Sortir 6 pièces de 20 centimes de sa poche pour acheter sa baguette qui vaut 1,20 € est beaucoup plus rapide que de taper sur son clavier 20×5, de constater que cela fait 100, puis de réfléchir qu’il faut rajouter 20, par exemple (si l’on tâtonne), ou même de taper directement 20×6.
– Réponse n°3 : sans utilisation de méthodes de calculs rapides il n’aurait pas été possible de concevoir des machines qui ont désormais la capacité d’afficher un résultat instantanément, comme votre smartphone par exemple !
Ce sont ces idées-ci que vous, parents, pouvez transmettre à vos enfants.
Apprendre ses tables de multiplication est certes parfois fastidieux mais cela ne sert pas à rien ! Cela nous sert à obtenir rapidement des résultats sans avoir à faire de longs calculs.
Cela évite de faire des additions successives lorsque l’on a besoin d’ajouter plusieurs fois la même quantité.
Aussi, point important : cela sera indispensable lorsque les notions de divisions et de fractions seront étudiées. Vous venez d’acheter un sachet contenant 27 billes. Vous souhaitez les répartir équitablement entre chacun de vos trois enfants. Allez-vous prendre le temps de donner une bille à chacun neuf fois ou bien piocherez-vous 9 billes à 3 reprises ? Si vous connaissez vos tables de 3 et/ou de 9, pas de doute !
1.2 Avant d’apprendre ses tables : comprendre que multiplier c’est finalement additionner

Comme mentionné plus haut, une multiplication est en fait une opération qui nous permet d’estimer beaucoup plus rapidement des quantités que nous pourrions compter !
Imaginons le cas suivant. Paul reçoit en cadeau un sachet de billes. Il aimerait savoir combien ce sachet contient de billes. Il verse alors le contenu de son sachet sur la table. Il a alors plusieurs possibilités pour compter les billes : les compter une par une, ou bien deux par deux ou encore trois par trois, etc. Il est alors aisé de comprendre que regrouper des billes permet de compter plus rapidement ! Si Paul ne sait pas compter de 2 en 2 ou 3 en 3, etc., il peut effectuer des tas de billes de même quantité et ensuite compter les tas. Par exemple, s’il arrive à matérialiser 6 tas de 5 billes, il pourra ainsi dire qu’il a 6 fois 5 billes, soit 30 billes dans son sachet.
Si votre enfant a du mal à concevoir cela, n’hésitez pas à l’inviter à compter de cette manière ses voitures, ses billes, ses crayons, ses perles, ses cartes de jeu, etc. ! Vous pouvez l’aider en lui donnant des consignes. Par exemple : « je te lance un défi : compte toutes ces perles en faisant d’abord des paquets de 8 perles avant de compter ensuite le nombre de paquets ».
Surtout aidez-le à verbaliser ensuite son résultat : « regarde, tu as réparti les perles en 5 tas de 8 perles, et il reste deux perles toutes seuls. Tu as donc 5 fois 8 perles et deux toutes seules. Cela fait combien de perles en tout ? »
Si, à ce stade votre enfant ne connaît pas bien ses tables, n’hésitez pas à vous référer, avec lui, aux tables de multiplication écrites dans son cahier d’école, ou bien à une table de Pythagore (voir un peu plus loin dans l’article) ou même en utilisant une calculatrice. L’important n’est pas ici de connaître le résultat mais de comprendre ce qu’est une multiplication : la multiplication est une opération qui permet d’éviter une addition répétée.
Vous pouvez aller plus loin ensuite et faire remarquer que 5 paquets de 8 perles et 8 paquets de 5 perles représentent la même quantité de perles. Pour cela prenez les 5 tas de 8 perles, puis invitez votre enfant à mélanger toutes les perles avant de lui demander de constituer 8 paquets de 5 perles. Il verra ainsi que toutes les perles sont utilisées de la même façon et pourra vérifier dans son cahier ou avec la calculatrice que 8 fois 5 fait 40, comme 5 fois 8 !
Une autre manipulation permet d’arriver à ce type de résultat. Celle-ci est plutôt gourmande !
Plutôt que des paquets ou des tas d’objets, imaginez un tableau avec des lignes et des colonnes. Pas besoin de le dessiner, prenez une tablette (complète) de chocolat !
Par exemple, une tablette Lindt de chocolat au lait compte 4 carreaux de chocolat sur un côté ; et 5 de l’autre. Cela forme donc un rectangle de 4 colonnes et 5 lignes si l’on pose la tablette verticalement ou bien de 5 colonnes et de 4 lignes si on la regarde horizontalement. On a 4 fois 5 carreaux de chocolat dans un sens et 5 fois 4 carreaux de chocolat dans l’autre. Ce que revient à dire que 4×5 = 5×4. Et le cahier ou la calculatrice nous indique bien que cela donne le même résultat puisque 4×5=20 et 5×4=20. CQFD !
(NB : CQFD est un signe qui permet d’écrire rapidement « Ce qu’il fallait démontrer », une notation que l’on emploie dans les « grandes classes » lorsque l’on résout un problème à partir d’une démonstration).
1.3 Le sens de la multiplication : une question qui fait débat !

(Il s’agit ici d’un petit aparté qui complique un peu l’apprentissage des tables…)
Comment lisez-vous ceci « 2×6 » ? Et « 5×3 » ?
Il est fort probable que votre réponse soit : « 2 fois 6 » et « 5 fois 3 ». Et bien pas forcément !
Et « 5×3 » ?
Il est fort probable que votre réponse soit : « 2 fois 6 » et « 5 fois 3 ». Et bien pas forcément !
Selon plusieurs mathématiciens, 5×3 se lit « 5 multiplié par 3 » et non pas « 5 fois par 3 ».
Certes le résultat est le même mais si vous manipulez des quantités, cela change tout !
« 5 multiplié par 3 » (qui s’écrit aussi 5×3) c’est avoir 5 choses trois fois (ou 5 choses en trois exemplaires) ou, dit autrement : constituer 3 paquets de 5 choses. C’est également écrire 5+5+5 c’est à dire 5 additionné trois fois.
« 3 multiplié par 5 » (qui s’écrit aussi 3×5) c’est avoir 3 choses cinq fois (ou 5 choses en trois exemplaires)…
D’où l’intérêt de mettre l’accent sur le fait que 3 paquets de cinq billes représentent la même quantité que 5 paquets de trois billes, par exemple. Le résultat est 15 billes dans les deux cas.
Cette notion, appelée « commutativité » est importante.
=> dire que la multiplication est commutative, cela signifie – dans le cas de la multiplication – que pour n’importe quels nombres a et b, on a toujours a×b=b×a).
Elle est notamment importante car elle permet d’envisager que l’apprentissage des tables peut être rapide dans la mesure où de nombreuses multiplications se répètent (2×6 et 6×2 ont le même résultat : 12, 3×7 et 7×3 ont le même résultat : 21, etc.).
Il est toutefois intéressant de noter que selon le sens donné à une multiplication, sa compréhension peut être différente. Voici un exemple lu dans un document destiné à des enseignants, document rédigé par Jean-Luc Despretz, conseiller pédagogique de circonscription (CPC) de Landivisiau.
« (Evaluation CE2-2000) : l’élève devait calculer mentalement le produit 13×2 et la consigne demandée à l’enseignant était de « dicter 13×2 » (sans aucune autre indication sur les mots à prononcer). Une enquête auprès d’enseignants montre que ceux-ci ont dicté de trois manières différentes : « treize fois deux » ; « deux fois treize » et « treize multiplié par deux ». Selon le choix effectué (particulièrement « deux fois treize »), les réussites des élèves ne sont pas identiques… »
Dans ce document, monsieur Despretz invite à « proposer une mémorisation des tables qui a du sens » car écrire 6 fois 2 = 12 après avoir écrit 5 fois 2 = 10 permet de comprendre qu’il suffit de rajouter une fois de plus 2 pour obtenir 12. De même, chercher le résultat de 7 fois 2, c’est rajouter 2 au résultat de 6 fois 2.

(c) Jean-Luc Despretz – CPC Landivisiau
Ce dossier est également disponible sous forme d’ebook téléchargeable :
https://6foisplus.com/telechargement-ebook-tables-de-multiplication
2/Apprendre ses tables de multiplication en fabriquant ses propres outils et ressources
2.1 La "table de Pythagore" : un document de référence

La « table de Pythagore » (oui oui, il s’agit bien du même mathématicien, philosophe et astronome de la Grèce antique qui a donné son nom au fameux théorème qui dit que si a, b et c sont les côtés d’un triangle rectangle, alors a2+b2 =c2 !) est un outil privilégié pour comprendre la commutativité et envisager le fait qu’apprendre ses tables de multiplication n’est pas si compliqué que cela !
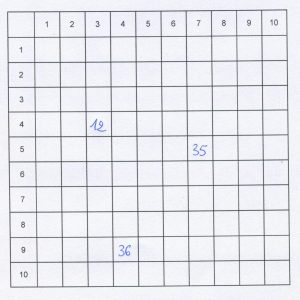
De quoi s’agit-il ? Il s’agit en fait d’un simple tableau composé de 11 lignes et 11 colonnes (en-têtes comprises) si l’on se réfère aux tables de multiplication allant jusqu’à 10. En haut, les en-têtes des colonnes (de 0 à 10), en horizontal les en-têtes des lignes, de 0 à 10 également. À l’intersection de chaque ligne et chaque colonne sont notés les résultats des multiplications, c’est-à-dire les produits.
Cette table de Pythagore a de nombreuses vertus. Elle permet notamment de comprendre que :
– la grande majorité des résultats sont notés deux fois du fait de la commutativité (2×3 = 3×2 = 6, le 6 est donc reporté deux fois : à l’intersection de la colonne 2 et de la ligne 3, et à l’intersection de la colonne 3 et de la ligne 2),
– après la table de 2, les tables de 4 et de 8 peuvent être reconstruites (idem après la table de 3 pour 6 et 9),
– la seule table n’ayant aucun lien avec les autres, donc a priori la plus difficile à mémoriser, c’est la table de 7 (mais que à part 7×7, tous les autres produits peuvent être retrouvés par commutativité ce qui revient à dire que seul le résultat de 7×7 est à apprendre !)
Et plusieurs choses peuvent être ensuite remarquées :
– le 0 « mange » tous les chiffres. Quand on multiplie par 0 le résultat est toujours 0,
– le 1 « ne change rien ». Quand on multiplie par 1, le chiffre ne change pas,
– lorsqu’on multiplie par 10 il suffit de « rajouter un 0 » après le chiffre à multiplier,
– multiplier par 2, revient à écrire le double du chiffre ou à compter de 2 en 2,
– multiplier par 4, c’est multiplier (ou doubler) les résultats de la table de deux,
– dans la table du 5, les résultats se terminent alternativement par 0 et 5,
– pour mémoriser la table du 9 on peut remarquer que les chiffres des unités décroissent quand les chiffres des dizaines croissent (le chiffre des dizaines avance toujours de 1, alors que le chiffre des unités recule toujours de 1).
Résultat : avec les carrés (les chiffres multipliés par eux-mêmes), finalement seuls quelques produits sont à réellement apprendre par cœur (par exemple apprendre que 2×3=6 suffit, connaître par cœur 3×2 n’est pas indispensable dans la mesure où l’on sait que cette opération donne le même résultat) !
Il ne s’agit pas ici d’imprimer une table de Pythagore remplie, comme on peut en trouver sur internet. Il est important que l’enfant remplisse lui-même les cases : d’abord pour réviser ses tables, ensuite pour se rendre compte – par lui-même – de tout ce qui est mentionné plus haut.
Bien sûr, n’hésitez pas à l’aider et à pointer du doigt certaines caractéristiques de la table. L’enfant ne doit pas être mis en échec. Il doit prendre du plaisir à fabriquer son propre outil. Outil auquel il pourra se référer lorsqu’il ne sera pas sûr de lui.
Il est même possible d’y ajouter deux glissières (une verticale et l’autre horizontale) pour que le résultat d’une multiplication donnée ressorte de façon très visuelle.
2.2 Des tables de multiplication simplifiées : pour ne visualiser que ce qui est vraiment à retenir par cœur

Tables de multiplication simplifiées proposées par le site apprendreamultiplier.com.
Comme mentionné ci-dessus, il est possible d’envisager l’apprentissage des tables de multiplication de manière allégée, ce qui peut rassurer un enfant en panique dès qu’il est face à tout ce qu’il doit apprendre.
Le site apprendreamultiplier.com propose une démarche tout à fait intéressante pour rassurer les enfants qui ont du mal ou pensent avoir du mal à tout apprendre par cœur.
En faisant abstraction de tous les doublons et des résultats des tables de 0, 1 et 10 (que l’on n’a pas vraiment besoin de mémoriser), seuls 36 résultats sont à apprendre, ce qui avouons-le fait beaucoup moins peur que si l’on considère qu’il y a 100 résultats à connaître !
Le site apprendreamultiplier.fr offre en téléchargement gratuit une feuille récapitulant les 36 résultats à mémoriser.
2.3 Des cartes mentales pour apprendre les tables de multiplication difficiles

Les cartes mentales, aussi appelées cartes heuristiques ou encore mind maps, en anglais, permettent de poser sur le papier des informations de manière très visuelle. Au centre de la feuille figure le sujet que l’on veut décliner. De ce sujet partent des « branches » (ou ramifications) permettant de le décliner en sous-sujet (ou sous-catégorie), un sous-sujet par branche. Et chaque branche peut elle-même donner lieu à d’autres branches. Se dessine ainsi un schéma, censé refléter un cheminement de pensée. Et tout est permis : couleurs, dessins, branches arrondies ou droites : l’important est de rendre visuelle l’information qui peut ainsi plus aisément être organisée et comprise (si le schéma n’est pas trop dense) et mémorisée (surtout pour celles et ceux qui ont besoin de « voir » les choses pour les retenir).
Bien sûr lire des cartes mentales peut aider celui qui apprend. Pour autant, il nous semble que l’apprentissage est plus efficace si l’apprenant écrit lui-même ses propres cartes mentales.
Ainsi, inviter votre enfant à faire ce type de schéma. Prenons un exemple avec pour sujet principal 7×8=56. L’idée est alors de placer 7×8=56 au centre de la feuille, dans un cercle, un nuage ou toute autre forme qui plaira à l’enfant. Partent ensuite de ce sujet des ramifications. Dans notre exemple, il est notamment possible de prévoir différents types de ramifications comme :
– la multiplication inversée : 8×7=56,
– l’addition qui peut mener à ce résultat : 7+7+7+7+7+7+7+7,
– un dessin de 8 paquets contenant chacun 7 points,
– un rectangle qui comprend 7 lignes et 8 colonnes.
Ce dossier est également disponible sous forme d’ebook téléchargeable :
https://6foisplus.com/telechargement-ebook-tables-de-multiplication
2.4 Apprendre ses tables en fabricant des jeux de société

Fabriquer ses propres jeux de société a deux vertus :
– aider à apprendre certaines notions (puisqu’il faut réfléchir à ce que l’on doit écrire sur les fiches de consignes ou les cartes de jeu, et puisque cela fait intervenir la graphie, donc le geste, une voie qu’il ne faut pas négliger en particulier pour les profils dit « kinesthésiques »),
– offrir un moment qui allie plaisir et révision des notions apprises lorsqu’il faut tester le jeu !
Voici quelques exemples de jeux très simples à réaliser :
— Création d’un jeu de memory (« mémo ») des tables de multiplication
Le jeu de memory offre l’opportunité de jouer avec des paires. Le principe du jeu : retrouver des paires de cartes identiques parmi un certain nombre de cartes disposées face cachée. Nous vous proposons ici non pas de créer des paires de cartes identiques mais de créer des paires de cartes ayant le même résultat. Par exemple la carte « 2×3 » devra être associée à la carte « 6 », etc.
Pour ne pas avoir un jeu avec trop peu de cartes (si l’on crée par exemple un mémo pour une table donnée) ou avec trop de cartes (un jeu avec toutes les tables de multiplication), nous vous proposons de ne tenir compte que des associations qui posent problème à votre enfant : par exemple « 7×8 » et « 56 », « 8×9 » et « 72 », etc., et de constituer ainsi 20 à 30 paires (pas plus).

Découpez, par exemple, 40 cartes de 5×5 cm de côté dans des fiches bristol. Invitez ensuite votre enfant à prendre deux cartes, puis à inscrire sur l’une une multiplication qu’il a du mal à retenir (par exemple 7×8) et sur l’autre le produit (ici 56). Et ainsi de suite. S’il a de réelles difficultés, il peut noter « 7×8=56 » sur la première carte et, sur la seconde carte, « 56 », avec entre parenthèses et en plus petit, « 7×8 ». Il peut aussi écrire ces chiffres de la même couleur et changer de couleur pour chaque paire de cartes.
— Création d’un jeu de Mistigri des tables de multiplications
Dans un classique jeu de Mistigri, les joueurs, cartes en main, regardent s’ils peuvent constituer des paires et les éliminent de leur jeu. La partie débute ensuite. Chaque joueur à son tour présente son jeu, cartes cachées, à son voisin qui prend une carte. S’il peut former une nouvelle paire avec cette carte, il l’élimine de son jeu. Le joueur qui se retrouve avec la carte « Mistigri » perd la partie !
Découpées, par exemple, dans des fiches Bristol, les paires peuvent ainsi être matérialisées par des multiplications et leur produit ! Comme dans le jeu de « mémo » décrit plus haut, l’enfant peut se focaliser sur les multiplications qu’il a du mal à retenir et constituer ainsi une quinzaine de paires (et prévoir, en plus, une carte « Mistigri » qu’il personnalisera à sa manière).
— Création d’un jeu de l’Oie des tables de multiplications
Le jeu de l’Oie est un jeu de plateau qui se joue depuis le XVIe siècle ! Soixante-trois cases réparties en spirale constituent le parcours que doit suivre chaque pion. Chaque joueur joue chacun son tour en lançant deux dés puis en avançant son pion d’autant de cases que de points indiqués par les dés. Mais certaines cases ont des règles spécifiques qui viennent perturber le cours du jeu.
L’idée est ici de proposer à l’enfant d’inventer ses règles, des règles qui doivent comprendre au moins une multiplication !
Par exemple, la case 6 peut donner la consigne suivante : « multipliez 6 par 3 et positionnez votre pion sur la case comportant le résultat de cette multiplication. Ne vous trompez pas, 6×3=18 ! ». La case 27 peut afficher la règle suivante : « 27 est un multiple de 9 (c’est un résultat de la table de 9). Reculez et positionnez votre pion sur la case n°3 car 9×3=27 », etc.
Et pour corser le jeu, n’hésitez pas à condamner les 6 et le 5 de l’un des dés (en posant, par exemple, une étiquette dessus) et dire qu’au lieu d’additionner les dés, on les multiplie (le dé à quatre faces visibles permettra de ne pas avancer trop vite sur le plateau). Le plateau pourra être dessiné par l’enfant sur une feuille A4 ou A3 (pour avoir plus de place) et les règles pourront être listées sur une feuille à part.
D’autres jeux ne nécessitant que des feuilles de papier et des stylos pour jouer vous sont également proposés dans cet article publié sur le site de 6foisplus.com dans l’article intitulé « Occuper ses enfants quand l’attente est longue et les exercer au calcul mental : 5 idées ludiques ».
3. Apprendre ses tables grâce aux pédagogies alternatives
3.1 Les tables de multiplication avec la méthode Montessori

La pédagogie Montessori s’appuie sur la manipulation et l’expérience avec le recours à du matériel propice au développement et à l’apprentissage de l’enfant par lui-même. La table perforée ainsi que les barrettes de perles présentées ci-après font partie du matériel utilisé en mathématiques. Parmi les particularités de l’ensemble du matériel Montessori figure le fait qu’il est sensoriel et qu’il est autocorrectif. Ce qui est le cas ici.
— La table perforée pour se rendre compte visuellement de ce qu’est une multiplication
La table perforée utilisée dans la pédagogie Montessori permet de visualiser très simplement ce que représentent les multiplications. Elle offre une approche visuelle de l’idée qu’une multiplication est une répétition d’un groupe d’objets, tout en permettant à l’enfant de manipuler des quantités de perles afin qu’il s’en rende compte par lui même .

Cette table perforée est en fait un plateau est en bois comportant 100 trous (disposés en 10 lignes et 10 colonnes) adaptées pour recevoir les perles que l’enfant doit compter (des perles de couleur rouge si l’on se réfère au matériel codifié de la pédagogie). Elle comporte aussi un trou plus grand en haut à gauche contenant un jeton (rouge également) qui est amené à être déplacé pour marquer la colonne du multiplicateur, ainsi qu’une encoche sur le côté gauche destinée à recevoir un carton qui indique le multiplicande.
En utilisant cette table perforée, l’enfant mémorise visuellement la disposition des perles lorsqu’il effectue une multiplication. Il peut voir, grâce aux perles, que le même nombre est répété à chaque fois. Il reporte ensuite le résultat dans une fiche. S’il n’est pas sûr de lui ou s’il veut vérifier qu’il a juste, il peut compter les perles qu’il a disposées sur le plateau.
Prenons un exemple. Celui de la table de 4. Voici ce que préconisent les auteurs de l ‘ouvrage Pas à Pas. « Glissez le carton du 4 dans l’encoche de la table, lisez la 1re opération (4 x 1 =). Posez le jeton rouge au-dessus de la colonne du multiplicateur 1 et placez 4 perles dans les trous de la colonne du 1. Comptez les 4 perles à voix haute, dites « 4 que je prends 1 fois ou 4 multiplié par 1 = 4 » et écrivez le résultat de l’opération. Lisez la 2e opération « 4 que je prends 2 fois ou 4 multiplié par 2 ». Poussez le jeton au-dessus du 2 et ajoutez 4 perles. Pointez la 4e perle du résultat précédent et comptez à partir de 4 jusqu’à 8. Annoncez « 4 que je prends 2 fois ou 4 multiplié par 2 = 8″ et écrivez le résultat. L’enfant continue seul, même si vous restez à côté de lui comme secrétaire. »
— Les barrettes de perles pour l’aspect tactile, s’entraîner à multiplier et intégrer la notion de multiples
Utilisées pour aborder l’addition dans la pédagogie Montessori, les barrettes de perles de couleur permettent également d’intégrer visuellement – et par le toucher – le concept des tables de multiplication.
De quoi s’agit-il ? Souvent montées sur un axe métallique crocheté aux deux bouts (ou bien collées ou bien faites maisons et enfilées sur un fil de coton), les barres de perles colorées Montessori contiennent entre 1 et 9 perles accolées (1 perle rouge, 2 perles vertes, 3 perles roses, 4 perles jaunes, 5 perles bleu clair, 6 perles mauves, 7 perles blanches, 8 perles marron, 9 perles bleu marine selon la codification de la pédagogie)
(c) Céline Alvarez
Pour réaliser la multiplication 5 x 3, il suffit par exemple de prendre 3 barrettes de 5 perles et d’inviter l’enfant à compter le nombre de perles, en insistant également sur les multiples de cinq : 5, 10 et 15.
Ainsi, l’enfant peut constater qu’il s’agit d’additionner trois fois le mutliplicande. Avec ce matériel, il va également pouvoir constater que l’on compte de 5 en 5 (dans cet exemple de 5×3).
Il va « intégrer peu à peu sensoriellement le fait que lorsque l’on fait les tables de multiplication, on compte de multiple en multiple du multiplicande. Par exemple pour 6 x 4, on compte de 6 en 6 quatre fois : 6, 12, 18, 24. Il peut alors encore remplir des livrets de tables de multiplication et ainsi, sans apprendre par cœur, il apprendra les tables et aura surtout intégré le moyen mnémotechnique de toujours retrouver le résultat », indique Sylvie d’Esclaibes, spécialiste de la pédagogie Montessori, sur son site internet.
3.2 La méthode de Singapour

Depuis la publication, en 2015, des mauvais résultats de la France à l’évaluation Pisa (le « Programme international pour le suivi des acquis des élèves » de l’OCDE) et celle, en 2018, du rapport Villani-Torossian (« 21 mesures pour l’enseignement des mathématiques », rapport résultant d’une mission sur les mathématiques confiée à une équipe menée par Cédric Villani, député de l’Essonne, et Charles Torossian, inspecteur général de l’Education nationale, la méthode dite de Singapour fait parler d’elle.
Car à Singapour, les écoliers affichent de très bons résultats en maths… bien meilleurs qu’en France si l’on se réfère à l’évaluation Pisa.
Mais de quoi s’agit-il et qu’apporte la méthode de Singapour ?
Conçue dans les années 1980, cette méthode n’a pas été créée sur des bases nouvelles. L’idée : s’inspirer des pratiques existantes les plus efficaces pour mettre en place une méthode qui permettrait d’élever le niveau des maths des élèves singapouriens.
La méthode de Singapour repose ainsi sur divers travaux dont ceux de pédagogues occidentaux comme Jerome Seymour Bruner (pour le passage du concret à l’abstrait), Maria Montessori (pour l’usage de matériel) ou George Pólya (pour la résolution de problèmes).
Elle comporte trois axes principaux
– l‘approche “concrète-imagée-abstraite” en trois étapes
— une étape « concrète » qui permet de mettre en scène la situation mathématique étudiée,
— une étape « imagée » qui s’appuie sur la schématisation des objets concrets précédemment mis en situation,
— une étape « abstraite » qui introduit chiffres et symboles mathématiques.
– la résolution de problèmes (avec un problème et un résultat qui peuvent être modélisés à partir de petites barres exprimant de façon visuelle les quantités)
– la verbalisation (formulation à voix haute du raisonnement et échanger avec les autres).
Critiquée, l’adaptation française proposée par l’éditeur La Librairie des Ecoles a récemment fait l’objet d’une nouvelle édition. Selon l’éditeur, la version française des manuels 2019 tient compte des repères 2018 de l’Éducation nationale et des retours terrain des enseignants.
Quid des tables de multiplication avec la méthode de Singapour ?
Comme pour les autres opérations, le « sens des choses » est le point de départ. Avant d’introduire symboles ou techniques opératoires, il s’agit d’aider l’enfant à comprendre le sens de la multiplication. Sont ensuite introduits des objets de la vie qui permettent de manipuler concrètement des quantités. Arrive après l’étape de schématisation où les objets deviennent des points ou autres symboles de ce type. Enfin, l’opération mathématique est indiquée à l’enfant.
Si la méthode est à suivre pas à pas, de façon codifiée, pour les enseignants, rien ne nous empêche, nous, parents, de nous en inspirer (sans avoir l’obligation de la suivre à la lettre) ! D’ailleurs, vous pourrez noter que les conseils et astuces mentionnés au début de ce dossier mettent l’accent sur le sens donné aux opérations et la manipulation !
Une remarque toutefois. Pour les multiplications, la méthode de Singapour telle qu’elle est retranscrite en français ne semble pas se soucier du sens que l’on donne, en français, aux termes « multiplié par » et « fois ». Si l’on se réfère à la vidéo ci-dessous, Stella Baruck aurait sans doute écrit 2×3 et non 3×2 ! Cette confusion n’existe pas dans la méthode originale puisqu’elle est documentée et enseignée en anglais !
Ce dossier est également disponible sous forme d’ebook téléchargeable :
https://6foisplus.com/telechargement-ebook-tables-de-multiplication
4. Réviser ses tables en jouant
4.1 Des jeux de société classiques détournés

Il est possible de trouver sur internet, et plus particulièrement sur certains sites d’enseignants ou de parents qui font l’école à la maison, des jeux à imprimer (et éventuellement à plastifier.) Il s’agit souvent de jeux classiques détournés, à l’image
– du Dobble des tables de multiplications que l’on peut trouver sur le site Capuchon à l’école (http://capuchonalecole.eklablog.com/dobble-a125085630)
– du jeu de l’Oie proposé par le site https://aeshpourvousservir.blog4ever.com/jeu-de-l-oie-tables-de-multiplication
– du jeu de domino disponible sur le site : http://www.caracolus.fr/wp-content/uploads/sites/14/2015/12/dominos-multiplication.pdf
Un simple jeu de 54 cartes peut également suffire. Prenez un jeu de cartes classiques, enlevez les figures, considérez l’As comme un 1. Et c’est parti ! Vous pouvez jouer à un jeu de bataille : chacun dispose sa carte et celui qui donne le résultat de la multiplication en premier remporte le pli !
Vous pouvez également investir dans deux dés à 10 faces (de 0 à 9 ou bien de 1 à 10) pour des batailles de lancés de dés. Chacun lance son dé. Celui qui donne le résultat de la multiplication en premier remporte la manche ! Et ainsi de suite…
Bien sûr, ne nous privons pas des jeux préalablement fabriqués à la maison : Memory, Mistigri ou jeu de l’Oie !
4.2 Des jeux de société du commerce

Plusieurs jeux de société permettent aux enfants de réviser leur table de multiplication en jouant ! Nous vous en présentons quatre dans ce dossier mais un article consacré aux jeux, plus exhaustif, est en préparation (stay tuned !).
Tam Tam MultiMax
Comme lorsque vous jouez au Dobble, avec Tam Tam MultiMax il s’agit de retrouver l’unique point commun entre deux cartes : une multiplication et son résultat, un nombre qui figure sur les deux cartes ou bien une multiplication également présente sur la carte de chacun des adversaires.

Deux niveaux existent : Tam Tam MultiMax tables 2 à 5 et Tam Tam MultiMax tables 2 à 9. Un coffret avec les deux jeux est également commercialisé.
Folix
Médaille d’or au Concours Lépine en 2008, Folix ressemble au premier abord à un jeu de memory classique (110 jetons avec des chiffres sont à disposer face cachée sur le plateau), mais plutôt que de retrouver deux jetons mentionnant le même chiffre, il faut ici trouver les deux chiffres qui, multipliés l’un à l’autre, donnent le résultat indiqué sur une carte que l’on aura préalablement retournée.

Et pour pimenter le jeu, certains jetons n’ont pas de nombre et proposent des actions spéciales qui rendent le jeu très ludique et l’issue de la partie très incertaine. Pour celles et ceux qui ne maîtrisent pas encore bien leurs tables, les couleurs des cartes et des jetons peuvent aider les joueurs.
MathSumo
Médaille d’or au Concours Lépine 2011 / 2012 et nominé au prix EducaFlip 2016, MathSumo est un jeu tout simple mais très ludique et efficace !

Un plateau avec une zone d’affrontement (celle des sumotoris) comportant 11 emplacements numérotés de 0 à 10, deux sumotoris cartonnés, X cartes dont six distribuées à chacun des joueurs (le reste constituant la pioche) : la partie peut commencer ! L’objectif de chacun des joueurs : être le premier à ne plus avoir de cartes en main.
A chaque tour, un joueur sélectionne dans son jeu une carte qu’il pose sur le plateau afin de s’en débarrasser. Son objectif : réaliser une multiplication dont le résultat figure sur la carte. C’est la position des sumotoris qui indique les facteurs à multiplier. Mais, attention : un seul sumo peut être déplacé à la fois. Par exemple, si un joueur pose la carte 21 sur le plateau et qu’un sumo est déjà positionné sur la case 3, il peut poser le deuxième sumotori sur la case 7. En revanche, si l’un des pions sumos est posé sur la case numéro 2, il ne pourra rien faire et devra piocher une nouvelle carte. Bien sûr, des cartes spéciales peuvent chambouler le cours de la partie !
Ce jeu permet de partir des résultats pour réviser les tables avec une mécanique de mémorisation plutôt originale. Autre plus : sur les cartes, les nombres sont exprimés en chiffres et des carrés de couleur (qui rappellent les réglettes cuisenaires) offrent la possibilité de voir les multiplications possibles pour un même résultat.
Multipli Potion
Egalement primé au concours Lépine et nominé au prix EducaFlip 2017, Multipli Potion est un jeu de cartes original ! Le but est d’être le premier à capturer cinq monstres adverses.

Conçu par un enseignant, ce jeu comporte 64 cartes. Sur chaque carte, il y a un nombre « potion » et un nombre « monstre ». Le but du jeu est de réunir et de multiplier, à chaque tour, deux potions afin de capturer l’un des monstres de son adversaire. Les joueurs jouent tour à tour.
A chaque tour, le joueur possède trois cartes en mains et pioche une 4ème carte. Il pose la carte de son choix devant lui. Puis c’est au tour du joueur adversaire de procéder de la même façon. Dès qu’un joueur possède deux cartes potions dont le produit est égal à un nombre « monstre » du joueur adverse, il gagne la carte de son adversaire et remet ses deux cartes potions utilisées dans la pioche.
Une part de stratégie est de mise dans la mesure où il faut être vigilant afin de ne pas se faire capturer trop facilement ses cartes. Chaque joueur doit bien réfléchir avant de poser ses cartes sur la table !
5/ Réviser ses tables à haute voix
5.1 Les tables de multiplication mises en poèmes par Jean Tardieu

Le saviez-vous ? Jean Tardieu a publié, en 1947, un recueil de poésies ayant pour thème les tables de multiplication. Ce recueil, destiné aux enfants avait pour titre « Il était une fois, deux fois, trois fois … ou La table de multiplication en vers ». Cet ouvrage a été réédité par Gallimard sous le titre Je m’amuse en rimant ».
Pour donner un aperçu de ces charmantes poésies, voici celle de la table de 7 :
Les sept nains
La princesse Blanche-Neige,
Chez les sept nains qui la protègent,
Lave, nettoie, époussette,
Sept fois un, sept
Lorsqu’une vieille aux jambes torses,
Sept fois deux, quatorze,
Lui dit : « Prends ce beau fruit, tiens! »
Sept fois trois, vingt et un,
Mais un des nains frappe à la vitre,
Sept fois quatre, vingt-huit,
Et lui dit : « Garde-toi bien »,
Sept fois cinq, trente-cinq,
« De mordre à ce fruit dangereux »,
Sept fois six, quarante-deux,
« C’est un poison qu’elle t’offre! »
Sept fois sept, quarante-neuf,
La vieille, dans les airs, s’enfuit…
Sept fois huit, cinquante-six.
Et la Princesse des bois,
Sept fois neuf, soixante-trois,
Est sauvée par ses amis,
Sept fois dix, soixante-dix.
Ce type de poème, qui n’est pas si difficile à apprendre, pourra plaire à votre enfant. Notre conseil : lire toutes ces poésies et les réciter à haute voix.
Bien sûr, cela peut également donner des idées : pourquoi ne pas inviter votre enfant à écrire lui même quelques rimes en lien avec l’une des tables qu’il a le plus de mal à retenir ?
5.2 Inventer les paroles d’une chanson

Bien sûr, il n’est pas évident de composer un air original. Mais il est possible de détourner des airs bien connus pour leur donner de nouvelles paroles.
Prenons comme exemple « Promenons-nous dans les bois », une chansons connues de tous, et imaginons de nouvelles paroles :
2 fois 1, ça fait 2,
2 fois 3, ça fait 6,
2 fois 4, c’est 8
Et 2 fois 5, c’est 10 !
2 fois 6 égal 12
2 fois 7 c’est 14
2 fois 8 c’est 16
Et 2 fois 9, 18 !
Cet exercice est ludique et le fait de chercher à poser des paroles sur une mélodie peut aider l’enfant à retenir ses tables.
Ensuite il n’a plus qu’à chanter sa chanson et, l’air aidant, il retiendra à n’en pas douter les paroles !
6/ Mettre les tables de multiplication en images
6.1 Les cartes mentales : toute une histoire !

Nous avons déjà parlé, dans ce dossier, de cartes mentales. L’idée était d’inviter l’enfant à créer ses propres cartes mentales afin de donner du sens aux multiplications et à mieux retenir ses tables. Ici, il s’agit de se référer aux cartes mentales que proposent Stéphanie Eleaume Lachaud et Filf. Via leur site mescartesmentales.fr, elles ont fait des cartes mentales dédiées aux apprentissages scolaires leur spécialité.
Stéphanie Eleaume Lachaud et Filf développent différents coffrets sur divers sujets liés aux apprentissages. Edité par Eyrolles, celui sur les tables de multiplication est en librairie depuis juin 2019. Il contient des cartes mentales mais pas seulement ! Il comprend un livret d’accompagnement pour découvrir la méthode des cartes mentales et un ensemble d’activités ayant pour thème les tables de multiplication (des cartes effaçables pour tester ses connaissances, des jeux, etc.). Surtout, il offre des contes à raconter… en cartes mentales, histoire que le cerveau associe des informations du conte aux résultats des multiplications !
A noter : pour celles et ceux qui souhaitent également se créer leurs propres cartes mentales, mais qui ont du mal à partir d’une feuille blanche, des blocs prêts à l’emploi sont disponibles sur le site des auteurs du coffret !
6.2 Méthode Multimalin : des images mentales pour aider à retenir ses tables

Cette méthode créée par Matthieu Protin, professeur des écoles, semble très appréciée. Il s’agit d’apprendre les tables de multiplication avec les techniques de mémorisation des champions du monde de mémorisation : en se créant des images mentales.
Il ne s’agit pas, ici, de donner du sens aux nombres ou aux opérations – ce qui pose des difficultés à certains enfants, comme les enfants dyscalculiques, par exemple – mais de fournir des images mentales amusantes qui aideront à la mémorisation des tables. A chaque multiplication, un lieu et une image différente, avec des chiffres qui prennent vie et à qui il arrive des histoires pour le moins rocambolesques !
Un exemple ? Prenons l’opération 7×9. Le 7 devient un plongeoir. Le 9 devient un bonhomme avec une tête d’œuf. Le signe = épouse les vagues de la piscine. Le 9 plonge, se retourne pour devenir un 6, et se cogne la tête ! Il se fait des bosses en forme de 3, ce qui fait apparaître le résultat 63.
Les enfants découvrent les personnages et les histoires dans un livret. Ils peuvent ensuite regarder les saynètes sous forme de vidéos grâce à un DVD fourni. Enfin, un jeu de cartes permet de réviser tout ce qui a préalablement été appris.
7/ Si l’enfant n’arrive toujours pas à retenir ses tables : des astuces pour retrouver les résultats

Voici pêle-mêle quelques idées qui peuvent être salvatrices !
– Autorisez votre enfant à retrouver les résultats cherchés grâce à la table de Pythagore. Plus il utilisera cet outil, plus il aura de facilité à mémoriser ses tables. Et si ce n’est pas le cas, il retrouvera malgré tout les résultats recherchés de plus en plus rapidement.
– Invitez votre enfant à utiliser ses mains et ses doigts, comme cela est décrit dans les cartes Timul. Ces cartes de format cartes à jouer – utilisent à la fois des images mentales pour toutes les tables de multiplication en dessous de 5×5 et des astuces avec les mains pour les tables de multiplication au-dessus de 5×5. Chaque carte comporte une multiplication illustrée soit par une histoire, soit par une astuce pour retrouver le résultat avec ses mains.
La vidéo ci-dessous, illustre bien ce procédé de visualisation du résultat des multiplications à partir des doigts :
– Aidez votre enfant à retrouver le résultat des multiplications grâce à des additions et des soustractions. La multiplication 6×6=36 est acquise mais votre enfant bute sur 6×7 ? Invitez-le à ajouter une nouvelle fois 6 à 36 ! De la même façon, si votre enfant connaît bien la table de 10, rappelez-lui que celle de 9 n’est pas difficile. Pour trouver les résultats de la table de 9 : on multiplie le nombre initial par 10 (pour cela il suffit d’ajouter un 0 après le nombre que l’on multiplie par 10), puis on soustrait le nombre initial : 4×9 est égal à (4×10)-4 = 40-4 soit 36 ; 6×9 est égal à (6×10)-6=60-6, soit 54 !
Et voici d’autres astuces/tips qui peuvent aider à retrouver un résultat :
Comme préalablement mentionné dans ce dossier :
– le 0 « mange » tous les chiffres. Quand on multiplie par 0 le résultat est toujours 0,
– le 1 « ne change rien ». Quand on multiplie par 1, le chiffre ne change pas,
– lorsqu’on multiplie par 10 il suffit de « rajouter un 0 » après le chiffre à multiplier,
– multiplier par 2, revient à écrire le double du chiffre ou à compter de 2 en 2,
– multiplier par 4, c’est multiplier (ou doubler) les résultats de la table de deux,
– dans la table du 5, les résultats se terminent alternativement par 0 et 5,
– pour mémoriser la table du 9 on peut remarquer que les chiffres des unités décroissent quand les chiffres des dizaines croissent (le chiffre des dizaines avance toujours de 1, alors que le chiffre des unités recule toujours de 1).
Mais on peut également rajouter ceci :
– 6×4=24, 6×6=36, 6×8=48 : des rimes sont cachées dans la table de 6 !
– pour une multiplication donnée dont l’un des deux multiplicateurs est pair, on peut décomposer la multiplication : on multiplie le deuxième nombre uniquement par la moitié du nombre pair puis on considère que le résultat final est le double de ce résultat intermédiaire. Par exemple, 8×9 c’est 4×9 deux fois, 7×6 c’est 7×3 deux fois, etc.,
– le produit de deux nombres impairs est un nombre impair.
Conclusion
Ce dossier vous aura, je l’espère, convaincu : multiplier n’est pas une opération si difficile! Et apprendre ses tables de multiplication peut s’envisager de façon ludique !
La notion de plaisir est particulièrement importante. Pour autant, le plaisir de partager un moment privilégié et agréable avec un parent, un grand frère ou une grande sœur, ou un adulte dont l’enfant apprécie la compagnie est, selon moi, tout aussi essentiel car il crée une émotion positive favorable aux apprentissages.
Pour rester dans le ludique et terminer ce dossier consacré aux tables de multiplication, je vous propose un tout petit petit quiz que vous pourrez partager en famille :
1/ Qui a 3 cm de large et cuit pendant 3 minutes ? Un œuf, parce que 3×3=9 ! (Une devinette que l’on peut retrouver dans l’ouvrage Les tables de multiplication, enfin les retenir, un livre qui donne de nombreux repères ludiques de ce type, ainsi que dans les cartes Timul).
Et, pour les plus matheux d’entre vous :
2/ Quels sont les trois nombres positifs qui donnent le même résultat quand on les multiplie ET quand on les additionne ? Il s’agit de 1, 2 et 3 car 1 x 2 x 3 = 6 ET 1 + 2 + 3 = 6 !
Ce dossier est également disponible sous forme d’ebook téléchargeable :
https://6foisplus.com/telechargement-ebook-tables-de-multiplication


Merci pour ce dossier très complet et ludique !
Ma fille rentre dans les multiplications et je vais essayer de rendre tout ça concret.
Merci encore
Merci pour votre commentaire. N’hésitez pas à nous faire part de vos avancées !
Bonjour. Merci, super dossier. Je vais tenter pour mon loulou Anael en CP. C’est génial, je ne connaissais pas. Douce journée.
Ping : Le blog 6foisplus.com Apprendre les maths autrement en jouant avec MathSumo ! | Mattika